Kartesische und polare zweidimensionale Koordinatensysteme
Dieser Onlinerechner wandelt Polarkoordinaten in kartesische Koordinaten um, und auch umgekehrt.
Diese Webseite exisiert dank der Arbeit von den folgenden Menschen:
 | Timur
|
Stefan Roesner
|
Der Inhalt ist unter der Creative Commons Namensnennung / Weitergabe unter gleichen Bedingungen 3.0 (nicht portiert) lizenziert. Dies bedeutet, dass Sie diesen Inhalt unter den gleichen Lizenzbedingungen frei weitergeben oder ändern dürfen, jedoch mit Zuordnung zum Entwickler indem Sie einen Hyperlink auf Ihrer Webseite zu dieser Arbeit https://de.planetcalc.com/134/ platzieren. Des Weiteren ändern Sie bitte keine Verweise auf das Originalwerk (falls vorhanden) das in diesem Inhlat vorhanden ist.
Das kartesische Koordinatensystem in einer Ebene wird durch die Auswahl des Ursprungs (Punkt O) und der Achse (zwei geordnete Linien senkrecht zueinander die sich am Ursprungspunkt treffen) genutzt.
Daher kann jeder Punkt auf einer Ebene durch die Angabe von deren Koordinaten angeordnet werden, welche der Abstand vom Ursprungspunkt zu den senkrechten Projektionen dieses Punktes zur Achse sind.
Es gibt weitere Koordinatensysteme für zweidimensionale Räume, mit denen man den Standort eines Punktes mit zwei Nummern finden kann. Das häufigste genutzte nach dem kartesischen ist das Polarkoordinatensystem.
Das Polarkoordinatensystem in einer Ebene wird durch die Auswahl des Ursprungspunkt (Pol) und eines Strahls, auch als Polarachse bezeichnet.
Die Distanz R von jedem Punkt zu dem Pol wird als Radialkoordinate oder einfach als Radius bezeichnet. Der Winkel zwischen der Polarachse und dem Radius ist der Polarwinkel, Winkelkoordinate oder Azimut. Dies sind die Polarkoordinaten von dem Punkt.
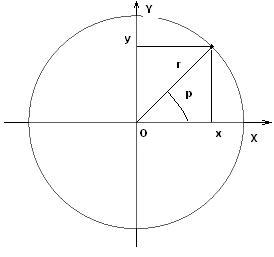
Die untenstehenden Rechner wandeln Polar- in kartesische Koordinaten um, und umgekehrt. Für die Berechnung wird angenommen, dass die Ursprungspunkte in beide Systemen gleich sind, und das die Polarachse entlang der positiven x-Achse verläuft.
Umwandlung von kartesischen Koordinaten in Polarkoordinaten
Kommentare