3D Koordinatensysteme
Diese Online-Rechner wandelt 3D-Koordinaten von/in kartesische, Zylinder- und Kugelkoordinaten
Der Inhalt ist unter der Creative Commons Namensnennung / Weitergabe unter gleichen Bedingungen 3.0 (nicht portiert) lizenziert. Dies bedeutet, dass Sie diesen Inhalt unter den gleichen Lizenzbedingungen frei weitergeben oder ändern dürfen, jedoch mit Zuordnung zum Entwickler indem Sie einen Hyperlink auf Ihrer Webseite zu dieser Arbeit https://de.planetcalc.com/7952/ platzieren. Des Weiteren ändern Sie bitte keine Verweise auf das Originalwerk (falls vorhanden) das in diesem Inhlat vorhanden ist.
Dieser Online-Rechner ist für die Koordinatentransformation von/in folgende 3D-Koordinatensysteme:
- Kartesische
- Zylindrischen
- Kugel
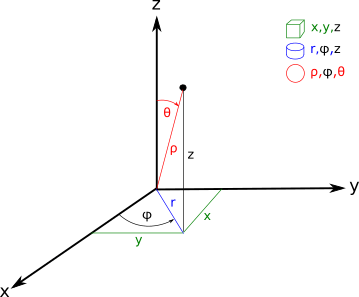
Kartesische, Zylinder und Kugelkoordinatensysteme
Kartesisches Koordinatensystem
Im kartesischen Koordinatensystem kann man einen Punkt mit 3 reellen Zahlen definieren: x, y, z. Jede Zahl entspricht dem vorzeichenbehafteten Mindestabstand entlang einer der Achsen (x,y oder z) zwischen dem Punkt und der Ebene, die durch die verbliebenen Achsen geformt wird. Die Koordinate ist negativ, wenn der Punkt hinter dem anfänglichen Koordinatensystem liegt.
Zylindrische Koordinatensystem
Dieses Koordinatensystem definiert einen Punkt in einer 3D-Fläche mit dem Radius r, Azimut φ und Höhe z. Die Höhe z entspricht direkt der z-Koordinate im kartesischen Koordinatensystem. Radius r ist eine positive Zahl, die kürzeste Distanz zwischen dem Punkt und der z-Achse. Der Azimut Winkle φ ist ein Winkelwert im Bereich 0-360. Es ist ein Winkel zwischen der positiven Semi-Achse x und dem Radius vom Ursprung zur Senkrechten vom Punkt zur xy-Ebene.
Kugelkoordinatensystem
Dieses System definiert einen Punkt in einer 3D-Fläche mit 3 reellen Werten – Radius ρ, Azimut Winkel φ, und Polarwinkel θ. Der Azimut Winkel φ ist der gleiche wie der Azimut Winkel im zylindrischen Koordinatensystem. Radius ρ ist die Distanz zwischen Ursprung des Koordinatensystems und des Punktes. Die positive Semi-Achse z und der Radius vom Ursprung zu dem Punkt formt den Polarwinkel θ.
Umwandlungsformeln für kartesische Koordinaten:
Radius im zylindrischen System:
Radius im Kugelsystem:
Azimut Winkel:
, siehe Zwei Argumtent-Arkustangens
Polarwinkel:
Umwandlungsformeln für zylindrische Koordinaten:
In kartesische Koordinaten:
,
Radius im Kugelkoordinatensystem:
Polarwinkel:
, siehe Zwei Argumtent-Arkustangens
Umwandlungsformeln für Kugelkoordinaten
Kartesische Koordinaten:
,
,
Radius im zylindrischen System:
Kommentare