Verhältnis von Wanderwellen
Das Verhältnis von Wellenfrequenz, Wellenlänge und Ausbreitungsgeschwindigkeit
Diese Webseite exisiert dank der Arbeit von den folgenden Menschen:
 | Timur
|
Stefan Roesner
|
Der Inhalt ist unter der Creative Commons Namensnennung / Weitergabe unter gleichen Bedingungen 3.0 (nicht portiert) lizenziert. Dies bedeutet, dass Sie diesen Inhalt unter den gleichen Lizenzbedingungen frei weitergeben oder ändern dürfen, jedoch mit Zuordnung zum Entwickler indem Sie einen Hyperlink auf Ihrer Webseite zu dieser Arbeit https://de.planetcalc.com/2348/ platzieren. Des Weiteren ändern Sie bitte keine Verweise auf das Originalwerk (falls vorhanden) das in diesem Inhlat vorhanden ist.
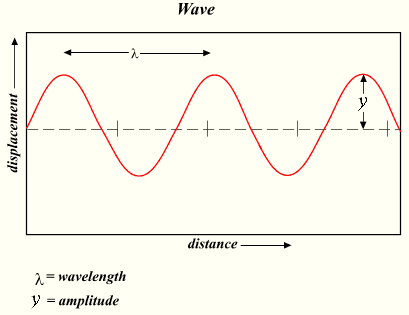
Wenn Sie einen Stein ins Wasser werfen, entstehen Wellen. Diese wandern heraus von dem Punkt, an dem der Stein das Wasser trifft. Wenn die Ausbreitungsgeschwindigkeit eine Konstante ist, wird die gewanderte Distanz aus Geschwindigkeit und Zeit berechnet. Die Wellenlänge ist die Distanz, die die Welle die Zeit gleich des Zeitraums wandert. .
Daher muss die Ausbreitungsgeschwindigkeit mit dem Zeitraum multiplizieren, um die Wellenlänger zu berechnen:
Mit der Nutzung der folgenden Definition von Frequenz
,
kann man die Standardverhältnis für eine Welle erhalten:
Der untenstehende Rechner berechnet die unbekannten Parameter anhand zwei bekannter.
Kommentare