Fläche eines Vierecks
Dieser Artikel beinhaltet mehrere Rechner für die Flächenberechnung eines Vierecks
Diese Webseite exisiert dank der Arbeit von den folgenden Menschen:
 | Timur
|
Stefan Roesner
|
Der Inhalt ist unter der Creative Commons Namensnennung / Weitergabe unter gleichen Bedingungen 3.0 (nicht portiert) lizenziert. Dies bedeutet, dass Sie diesen Inhalt unter den gleichen Lizenzbedingungen frei weitergeben oder ändern dürfen, jedoch mit Zuordnung zum Entwickler indem Sie einen Hyperlink auf Ihrer Webseite zu dieser Arbeit https://de.planetcalc.com/5977/ platzieren. Des Weiteren ändern Sie bitte keine Verweise auf das Originalwerk (falls vorhanden) das in diesem Inhlat vorhanden ist.
Es gibt verschiedene Methoden, um die Fläche eines Vierecks zu berechnen:
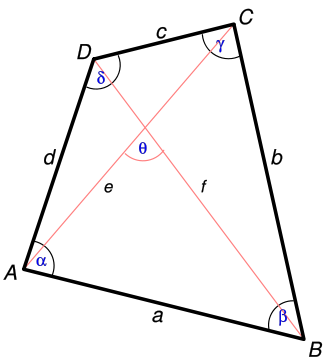
Bild: Wikipedia
- Fläche eines Vierecks mit vier gegebenen Diagonalen dem Winkel der diese trennt. In diesem Fall nutzt man die folgende Formel:
Rechner:
Konvexe viereckige Fläche
- Fläche eines Vierecks mit vier gegebenen Seiten und zwei gegenüberliegenden Winkel. In diesem Fall nutzt man die Formel von Bretschneider:
,
wobei s – Semiperimeter ist
Rechner:
Fläche eines Vierecks mit vier gebenenen Seiten und zwei gegenüberliegenden Winkel
- Fläche eines Vierecks mit vier gegebenen Seiten und zwei Diagonalen. In diesem Fall nutzt man die nicht-trigonomische Formel von Bretschneider
,
wobei s – Semiperimeter ist
Rechner:
läche eines Vierecks mit vier gebenenen Seiten und zwei Diagonalen
- Fläche eines zyklischen Vierecks mit vier gegebenen Seiten. Dies ist eine besondere Version der Formel von Bretschneider (man weiß, dass die Summe von den zwei gegenüberliegenden Winkel 180 Grad ergibt) - die Brahmagupta Formel.
,
wobei s – Semiperimeter ist
Für diese Berechnung können Sie den oberen Rechner nutzen, indem Sie beliebige Winkel, die 180 Grad ergeben, eingeben.
Der Beweis für die Formel von Bretschneider kann hier gefunden werden.
Es sollte auch erwähnt werden, dass es unmöglich ist, die Fläche eines Vierecks nur mit den vier Seiten zu berechnen. Sie brauche zusätzliche Information wie oben beschrieben. Da aber häufig danach gefragt wird, haben wir spaßeshalber einen Rechner erstellt, der die Fläche eines Vierecks nur mit vier gegebenen Seiten berechnet – für eine unendliche Anzahl von Vierecken. Sie können ihn im Fläche eines irreguräen Rechteck mit gegebenen Seiten finden.
Kommentare