PLANETCALC Online-Rechner

Anmeldung
StudieMathematikGeometrie

Einen Kreis schneiden

Diese Online-Rechner schneidet einen Kreis mit zwei verschiedenen Methoden in gleiche Teile: Sektorenschnitt und Parallelschnitt.

Diese Webseite exisiert dank der Arbeit von den folgenden Menschen:

Timur

Timur

SR

Stefan Roesner

Erstellt: 2021-09-12 05:27:08, Letzte Aktualisierung: 2021-09-12 05:27:08
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

Der Inhalt ist unter der Creative Commons Namensnennung / Weitergabe unter gleichen Bedingungen 3.0 (nicht portiert) lizenziert. Dies bedeutet, dass Sie diesen Inhalt unter den gleichen Lizenzbedingungen frei weitergeben oder ändern dürfen, jedoch mit Zuordnung zum Entwickler indem Sie einen Hyperlink auf Ihrer Webseite zu dieser Arbeit https://de.planetcalc.com/8943/ platzieren. Des Weiteren ändern Sie bitte keine Verweise auf das Originalwerk (falls vorhanden) das in diesem Inhlat vorhanden ist.

Unten kann man zwei Online-Rechner finden, die berechnen, wie man einen Kreis in gleiche Teile schneidet – mit einem traditionellen und nicht-traditionellen Methode. Mit der traditionellen Methode meinen wir das Schneiden des Kreises in Sektoren, wie man normalerweise eine Pizza schneidet. Die nicht-traditionelle Methode nehmen wir an, dass man den Kreis in gleiche vertikale Scheiben mit parallelen Linien oder parallelen Sehnen schneidet. Beide Rechner haben auch eine Zeichnung, um das Ergebnis grafisch darzustellen. Man kann alle Formeln in dem Artikel unter dem Rechner finden.

PLANETCALC, Einen Kreis in gleiche Sektoren schneiden

Einen Kreis in gleiche Sektoren schneiden

Zahlen nach dem Dezimalpunkt: 2
Winkel von einem Sektor
 
Bogenlänge eines Sektors
 
Sehnenlänge eines Sektors
 

PLANETCALC, Einen Kreis in gleiche Teilen mit einem parallelen Schnitt teilen

Einen Kreis in gleiche Teilen mit einem parallelen Schnitt teilen

Zahlen nach dem Dezimalpunkt: 2
Die Datei ist sehr groß; Beim Laden und Erstellen kann es zu einer Verlangsamung des Browsers kommen.

Einen Kreis in Sektoren schneiden

Man möchte einen Kreis in verschiedene Sektoren schneiden (auch ungerade Anzahlen). Um dies zu machen, muss man den Parameter für einen Sektor finden. Dies ist eine einfache Aufgabe:

  1. Ermittle den Winkle eines Sektors im Bogenmaß, indem man 2π (stellt 360 Grad des Bogenmaßes dar) durch die Anzahl von Sektoren teilt.
    \alpha=\frac{2\pi}{N}

  2. Ermittle die Bogenlänge eines Sektors durch das Multiplizieren eines Radius mit dem Winkel eines Sektors im Bogenmaß.
    a=\alpha R

  3. Ermittle die Sehnenlänge eines Sektors durch das Kosinus Gesetz (eine Sehne ist die Basis eines gleichschenkligen Dreiecks mit zwei Radien als Schenkel und Sektorenwinkel als Scheitelwinkel

c=R^2+R^2-2RR \cos \alpha
Diese Schritte bestimmen N gleich Sektoren.

Einen Kreis mit Parallelschnitten teilen

Diese Methode ist interessanter. Um es einfach zu halten, betrachten wir die Hälfte eines Kreises, da er symmetrisch ist.

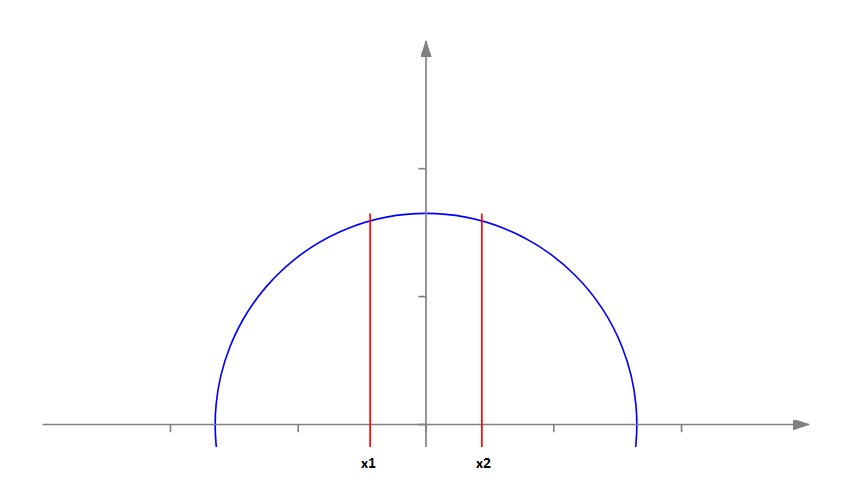
Einen Kreis in 3 Teile mit 2 parallelen Linien schneiden
Einen Kreis in 3 Teile mit 2 parallelen Linien schneiden

Wir schneiden den Kreis in vertikale Scheiben. In diesem Fall muss man die x-Koordinaten der parallelen Sehnen ermitteln, die den Kreis in gleichgroße Teile schneiden soll (siehe Punkte x1 und x2 im obigen Bild). Nun leitet man eine allgemeine Formel für die Fläche der linken Scheibe ab.

Der halbe Kreis kann man sich als Funktion y=f(x) vorstellen, wobei x die Koordinate entlang der Abszissenachse und y die Funktion gleich des Wertes des entsprechenden Halbkreispunktes ist.

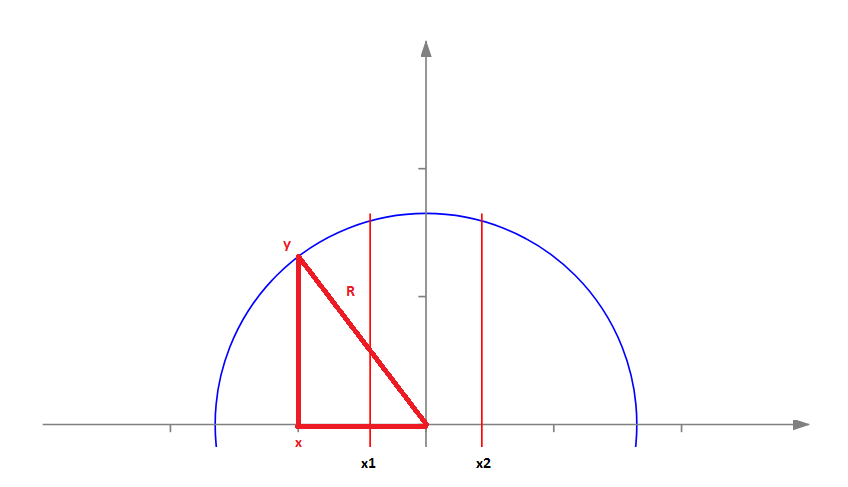
y=f(x)
y=f(x)

Unter der Verwendung des Satz des Pythagoras ist die y-Funktion

y=\sqrt{R^2 - x^2}}

Um die Fläche der linken Scheibe zu ermitteln, muss man die Funktion von -R zu x integrieren. Die Stammfunktion von unserer Funktion ist:

F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+C

Nun muss man den Wert der Konstanten finden. Offensichtlich sollte der Punkt, wo x gleich -R Fläche gleich Null sein. Wenn man dann -R anstatt von x in die obige Formal setzt, bekommt man

F(-R)=-\frac{\pi R^2}{4}+C=0, daher

C=\frac{\pi R^2}{4}

Das letzte Integral ist

F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}

Abe wie findet man x vom ersten Schnitt? Man kennt die Fläche, die man erhalten sollte – n-te Teil der Gesamtfläche (den Halbkreis beachten)

S=\frac{\frac{\pi R^2}{2}}{N}=\frac{\pi R^2}{2N}

Daher kann man es gleichsetzen mit

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}=\frac{\pi R^2}{2N}

Dies gibt dann

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}-\frac{\pi R^2}{2N}=0

Dies ist eine transzendentale Gleichung, und man benötigt ein numerisches Verfahren, um sie zu lösen, z.B. Bisektionsverfahren oder Newtonverfahren. Hier nutzen wir das Newtonverfahren.

Der nächste Punkt vom Schnitt kann man mit demselben Ansatz ermitteln. Für den zweiten Punkt S_2=2\frac{\pi R^2}{2N} muss man noch zweimal schneiden, für den dritten Punkt S_3=3\frac{\pi R^2}{2N} noch dreimal und so weiter und so fort.

Dann kann man alle anderen Parameter, wie die Sehnenlänge, anhand der Punktkoordinaten ermitteln.

URL zum Clipboard kopiert

Ähnliche Rechner

 #Geometrie #Kreis Bogen Fläche Geometrie Kreis Parallele Schnitt Sehne Sektor Winkel
PLANETCALC, Einen Kreis schneiden
Timur2021-09-12 05:27:08

Kommentare