Online-Rechner: Spiralrechner

Dies ist ein universeller Rechner für die archimedische Spirale.

Dieser Rechner hat fünf Dimensionen für eine Spirale: äußere Durchmesser - D, innere Durchmesser - d, Dicke, Trennungsabstand oder Abstand zwischen Armen – t, Spirallänge – L, Anzahl von Windungen – n. Diese Dimensionen sind miteinander verbunden (man kann die Formeln unter dem Rechner sehen), und es ist möglich jegliche 2 zu berechnen, solange man die anderen drei kennt.

Man sieht überall im täglichen Leben Spiralen in jedem Objekt sehen, das in einer gerollten Form ist: Papierrolle, Bänder, Filme etc. Man kann auch relativ einfach die Dimensionen der Objekte ermitteln, wie den Durchmesser, die Dicke, Anzahl der Windungen, und dann mit dem untenstehenden Rechner die restlichen Dimensionen berechnen. Zum Beispiel kann man die Rollenlänge anhand des äußeren oder inneren Durchmessers, Dicke oder Anzahl von Windungen berechnen. Man kann auch inverse Probleme (wenn man die Rollenlänge kennt) – berechne die Dicke und Anzahl von Windungen anhand der Rollenlänger und beider Durchmesser. Wie immer kann man die Formel und Theorie unter dem Rechner finden.
Bitte bei den Einheitengrößen aufpassen, wenn man die bekannten Dimensionen eingibt. 20 Meter sind nicht das gleiche wie 20 Millimeter…

Spiralrechner

Dimension

Wert

Dimension

Wert

Dimension

Wert

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 4

Spirallänge

innere Durchmesse

äußere Durchmesser

Dicke

Anzahl der Windungen

Archimedische Spirale

Die archimedische Spirale (auch als arithmetische Spirale bekannt) ist eine Spirale, die entsprechend den Positionen eines Punktes M, der sich vom Zentrumspunkt O mit einer konstanten Geschwindigkeit auf einer Linie OA, die um den Mittelpunkt O mit einer konstanten Drehbewegung rotiert, entsteht.

Wenn man den Abstand von O zu M als ρ und der Drehwinkel als φ, bezeichnet, dann beschreibt man eine Spirale mit einer Polargleichung:

$\rho = k \phi$ ,

wobei k die Parametergröße ist, die gleich der Änderung des Abstands ist, wenn der Winkel um 1 Bogenmaß rotiert. Nach einer Runde (ein Winkel vergrößert sich um 2π) vergrößert sich der Abstand um 2π.

$a = 2 \pi k$
Dies vergrößert den Abstand zwischen zwei Armen einer Spirale, Trennungsabstand oder Spiraldicke. Man kann die Ausgangsgleichung mit a umschreiben:

$\rho = \frac{a}{2 \pi} \phi$

Da die Dicke eine Konstante ist, gilt – je weiter sich der Punkt M vom Zentrum bewegt, desto mehr sieht die Spirale wie ein Kreis aus.

Um die Formel für die Spirallängen abzuleiten, muss man sich die infinitesimale Längenänderung anschauen.

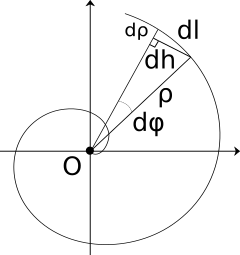
Ein infinitesimal Spiralsegment dl kann man sich als eine Hypotenuse von dl, dρ, und dh Dreieck vorstellen. Daher gilt:

$dl = \sqrt{d\rho^2+dh^2}$

Ein infinitesimal Spiralsegment kann man mit einem infinitesimalen Segment eines Kreises mit dem Radius ρ ersetzen; dann ist deren Länge ρdφ.

$dl = \sqrt{d\rho^2+\rho^2d\phi^2}$

Wenn man die Polargleichung einer Spirale verwendet, kann man ρ mit kφ, und dρ mit kdφ ersetzen

$dl = \sqrt{k^2d\phi^2+k^2\phi^2d\phi^2}=kd\phi\sqrt{1+\phi^2}=\frac{a}{2\pi}\sqrt{1+\phi^2}d\phi$

Nun hat man Abhängigkeit der Länge dl von dem Winkel dφ. Um die Länge zu ermitteln, muss man von dem Anfangswinkel zum Endwinkel integrieren.

$L=\int \limits _{\phi_0}^{\phi_1}\frac{a}{2\pi}{\sqrt {1+\phi ^{2}}}d\phi$

Um es kurz zu halten, die finale Ganzzahl ist:

$L=\frac{a}{2\pi}\left( \frac{\phi_1}{2}\sqrt{\phi_1^2+1}+\frac{1}{2}ln(\phi_1+\sqrt{\phi_1^2+1}) - \frac{\phi_0}{2}\sqrt{\phi_0^2+1}-\frac{1}{2}ln(\phi_0+\sqrt{\phi_0^2+1}) \right)$

Wenn eine Spirale von einem Grad Null (vom Center) anfängt, ist die Formal vereinfacht:

$L=\frac{a}{2\pi}\left( \frac{\phi_1}{2}\sqrt{\phi_1^2+1}+\frac{1}{2}ln(\phi_1+\sqrt{\phi_1^2+1}) \right)$

Aber im wirklichen Leben fängt eine Rolle natürlich nicht vom Center aus an. Normalerweise hat es eine Hülle, daher gibt es einen inneren Durchmesser und einen Anfangswinkel. Aber wie hängen diese Parameter miteinander zusammen?

Hier sieht man, wie die Anzahl der Windungen n mit den Winkeln zusammenhängt:

$n = \frac{\phi_1-\phi_0}{2\pi}$

Und hier sieht man, wie die Durchmesser und die Winkel zusammenhängen (dies folgt direkt der Polargleichung einer Spirale)

$D = \frac{a}{\pi}\phi_1 \\ d = \frac{a}{\pi}\phi_0$

Dies sind alle Formeln, die man benötigt, um die unbekannten Dimensionen anhand der bekannten Dimensionen zu ermitteln. Jedoch sollte man beachten, dass die Längengleichung transzendental ist, und die umgekehrte Aufgabe (das Finden von unbekannten Dimensionen, wenn die Länge bekannt ist) die numerischen Verfahren benötigt. Dafür sollte man den Sekanten-Verfahren Rechner verwenden.

PLANETCALC Online-Rechner

Spiralrechner

Diese Webseite exisiert dank der Arbeit von den folgenden Menschen:

Timur

Stefan Roesner

Spiralrechner

Archimedische Spirale

Ähnliche Rechner

Kommentare

PLANETCALC Online-Rechner

Spiralrechner

Archimedische Spirale

Ähnliche Rechner

Kommentare

Teilen diese Seite