Volumen von geometrischen Formen
Berechnet das Volumen von geometrischen Formen: Würfel, Prisma, Pyramide, Kegelstumpf, Kegel, Zylinder, Kugel, Ellipsoid
Der Inhalt ist unter der Creative Commons Namensnennung / Weitergabe unter gleichen Bedingungen 3.0 (nicht portiert) lizenziert. Dies bedeutet, dass Sie diesen Inhalt unter den gleichen Lizenzbedingungen frei weitergeben oder ändern dürfen, jedoch mit Zuordnung zum Entwickler indem Sie einen Hyperlink auf Ihrer Webseite zu dieser Arbeit https://de.planetcalc.com/131/ platzieren. Des Weiteren ändern Sie bitte keine Verweise auf das Originalwerk (falls vorhanden) das in diesem Inhlat vorhanden ist.
Dieser Artikel beinhaltet eine Sammlung von Rechnern zur Berechnung vom Volumen für geometrische Formen. Die Hauptquelle für die Berechnungsformeln: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum's Outline series in Mathematics. McGraw-Hill Book Co., 1968.
Volumen eines Würfels
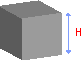
Formel:
Volumen eines rechteckigen Prismas
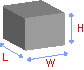
Formel:
Volumen einer Pyramide
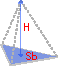
Formel:
Volumen eines Kegelstumpfes
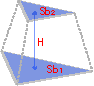
Formel:
Volumen eines Kegels
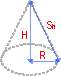
Formel:
Volumen eines Zylinders
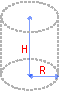
Formel:
Volumen einer Kugel
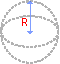
Formel:
Volumen eins Ellipsoids
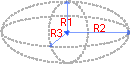
Formel:
Volumen eines Torus
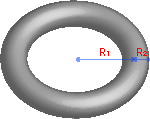
Formel:
Kommentare