Online-Rechner: Volumen von geometrischen Formen

Volumen von geometrischen Formen

Berechnet das Volumen von geometrischen Formen: Würfel, Prisma, Pyramide, Kegelstumpf, Kegel, Zylinder, Kugel, Ellipsoid

Dieser Artikel beinhaltet eine Sammlung von Rechnern zur Berechnung vom Volumen für geometrische Formen. Die Hauptquelle für die Berechnungsformeln: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum's Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Volumen eines Würfels

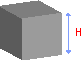
Formel: $V=H^3$

Volumen eines Würfels

Seite (H)

Seitenlänge

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 5

Volumen

Volumen eines rechteckigen Prismas

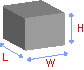
Formel: $V=HWL$

Volumen eines rechteckigen Prisma

Breite (B)

Höhe (h)

Länge(L)

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 5

Volumen

Volumen einer Pyramide

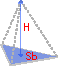
Formel: $V={1 \over 3} S_b H$

Volumen einer Pyramide

Basisfläche (Sb)

Fläche der Pyramidenbasis

Höhe (h)

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 5

Volumen

Volumen eines Kegelstumpfes

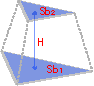
Formel: $V={H\over3}(S_{b1}+S_{b2}+\sqrt{S_{b1} S_{b2}})$

Volumen eines Kegelstumpfes

Basisfläche 1 (Sb1)

Basisfläche 2 (Sb2)

Höhe (h)

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 5

Volumen

Volumen eines Kegels

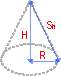
Formel: $V={1 \over 3} \pi R^2 H$

Volumen eines Kegels

Radius

Höhe (h)

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 5

Volumen

Volumen eines Zylinders

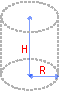
Formel: $V=\pi R^2 H$

Volumen eines Zylinders

Höhe (h)

Radius

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 5

Volumen

Volumen einer Kugel

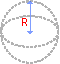
Formel: $V={ 4\over3 } \pi R^3$

Volumen einer Kugel

Radius

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 5

Volumen

Volumen eins Ellipsoids

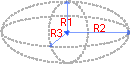
Formel: $V={4\over 3} \pi R_1 R_2 R_3$

Volumen einesr Ellipsoid

Radius 1 (R1)

Radius 2 (R2)

Radius 3 (R3)

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 5

Volumen

Volumen eines Torus

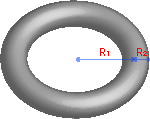
Formel: $V=2 \pi^2 R_1 R_2^2$

Volumen eines Torus

Radius 1 (R1)

Radius 2 (R2)

Präzesionsberechnung

Zahlen nach dem Dezimalpunkt: 5

Volumen

PLANETCALC Online-Rechner

Volumen von geometrischen Formen

Diese Webseite exisiert dank der Arbeit von den folgenden Menschen:

Anton

Stefan Roesner

Timur

Volumen eines Würfels

Volumen eines Würfels

Volumen eines rechteckigen Prismas

Volumen eines rechteckigen Prisma

Volumen einer Pyramide

Volumen einer Pyramide

Volumen eines Kegelstumpfes

Volumen eines Kegelstumpfes

Volumen eines Kegels

Volumen eines Kegels

Volumen eines Zylinders

Volumen eines Zylinders

Volumen einer Kugel

Volumen einer Kugel

Volumen eins Ellipsoids

Volumen einesr Ellipsoid

Volumen eines Torus

Volumen eines Torus

Ähnliche Rechner

Kommentare

PLANETCALC Online-Rechner

Volumen eines Würfels

Volumen eines Würfels

Volumen eines rechteckigen Prismas

Volumen eines rechteckigen Prisma

Volumen einer Pyramide

Volumen einer Pyramide

Volumen eines Kegelstumpfes

Volumen eines Kegelstumpfes

Volumen eines Kegels

Volumen eines Kegels

Volumen eines Zylinders

Volumen eines Zylinders

Volumen einer Kugel

Volumen einer Kugel

Volumen eins Ellipsoids

Volumen einesr Ellipsoid

Volumen eines Torus

Volumen eines Torus

Ähnliche Rechner

Kommentare

Teilen diese Seite